Notice
suyeonme
[자료 구조] 트리(Tree) 본문
트리(Tree)란?

- 데이터 사이의 계층 관계를 나타내는 자료구조이다.
- 트리를 구성하는 요소는 노드(node)와 가지(edge)이다. 각각의 노드는 가지로 연결되어있다.
- 그래프(Graph)의 여러 구조 중 무방향 그래프의 한 구조이다.
- 하나의 데이터 뒤에 여러개의 데이터가 존재할 수 있는 비선형 구조이다. (선형 구조: 데이터를 순차적으로 나열)
- 트리 구조는 계층적으로 표현이 되고, 아래로만 뻗어나가기 때문에 사이클(cycle)이 없다.
- 트리를 사용한 대표적인 예시로, 파일 시스템(File System)이 있다. 파일 시스템에서 폴더는 루트 폴더에서 시작되어 가지를 뻗어나가는 모양을 한다.
트리 관련 용어
| 용어 | 설명 |
| 루트(root) | 트리의 가장 윗부분에 위치하는 노드로, 하나의 트리에는 하나의 루트가 존재한다. |
| 리프(leaf) | 트리의 가장 아랫부분에 위치하는 노드로, 노드가 더이상 뻗어나가지 않는 마지막에 위치한다. |
| 안쪽 노드(non-terminal node) | 리프를 제외한 나머지 노드(루트 포함) |
| 자식(child) | 어떤 노드에서 가지로 연결된 아래쪽 노드로, 노드는 자식을 여럿 가질 수 있다. |
| 부모(parent) | 어떤 노드에서 가지로 연결된 위쪽 노드로, 각 노드에서 부모는 하나뿐이다. |
| 형제(sibling) | 부모가 같은 노드 |
| 조상(ancestor) | 어떤 노드에서 위쪽으로 뻗어나간 모든 노드 |
| 자손(descendant) | 어떤 노드에서 아랫쪽으로 뻗어나간 모든 노드 |
| 레벨(level) | 루트로부터 얼마나 떨어져있는지 나타낸 값으로 루트에서 가지가 아래로 뻗어나갈 때마다 레벨이 1씩 증가한다. |
| 차수(degree) | 노드가 갖는 자식의 수이다. 모든 노드의 차수가 n이하인 트리를 n진 트리라고 한다. |
| 높이(height) | 루트에서 가장 멀리 떨어진 리프까지의 거리(리프 레벨의 최댓값) |
| 서브트리(subtree) | 트리 안에서 어떤 노드를 루트로 정하고 그 자손으로 이루어진 트리 |
| 널트리(null tree) | 노드가 전혀 없는 트리 |
순서 트리(Ordered Tree)와 무순서 트리(Unordered Tree)
순서 트리(Ordered Tree)란?
형제 노드의 순서를 따지는 트리
순서 트리의 탐색
BFS와 DFS는 모든 노드를 한번만 방문한다는 공통점을 가지고 있다. 하지만 각각 장단점이 다르기 때문에 상황에 맞는 탐색기법을 사용해야한다.

너비 우선 탐색(breadth-first-search, BFS), 가로형 탐색
- 낮은 레벨에서 시작해 왼쪽에서 오른쪽 방향으로 따라가다가 한 레벨에서 탐색이 끝나면 다음 레발로 내려가는 탐색이다.
- 주로 두 정점 사이의 최단 경로를 찾을 때 사용한다.
- 만약, 경로를 하나씩 전부 방문한다면, 최악의 경우에는 모든 경로를 다 살펴보아야 한다
깊이 우선 탐색(depth-first-search, DFS), 세로형 탐색
- 리프에 이를때까지 아래로 내려가면서 탐색한다. 리프에 도달해 더 이상 탐색할 곳이 없으면 부모에게 돌아간다.
- BFS보다 탐색 시간은 조금 오래 걸릴지라도 모든 노드를 완전히 탐색할 수 있다.
깊이 우선 탐색의 순회 종류

깊이 우선 탐색을 진행하면서 '언제 노드를 방문할지'는 아래 세 종류로 구분된다.
- 전위 순회(preorder): 노드 방문 -> 왼쪽 자식 -> 오른쪽 자식
- 중위 순회(inorder): 왼쪽 자식 -> 노드 방문 -> 오른쪽 자식
- 후위 순회(postorder): 왼쪽 자식 -> 오른쪽 자식 -> (돌아와) 노드 방문
무순서 트리(Unordered Tree)
형제 노드의 순서를 따지지 않는 트리
이진트리(Binary Tree)란?
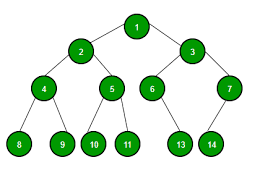
이진 트리란, 각 노드가 왼쪽 자식과 오른쪽 자식 둘을 갖는 트리이다. 이 때 두 자식 가운데 한쪽이 없거나 둘다 없는 노드가 포함되어도 된다. 이진 트리의 특징은 왼쪽 자식과 오른쪽 자식을 구분한다는 점이다.
완전이진트리(Complete Binary Tree)란?
완전이진트리란, 루트에서 아래쪽 레벨로 내려가는 노드가 빠짐없이 채워져있고, 또 같은 레벨에서는 왼쪽에서 오른쪽으로 노드가 빠짐없이 채워져있는 이진트리이다. n개의 노드를 저장할 수 있는 완전이진트리의 높이는 log n이다.
아래 조건을 만족해야한다.
1. 마지막 레벨을 제외한 레벨은 노드를 빠짐없이 가득 채운다.
2. 마지막 레벨은 왼쪽부터 오른쪽 방향으로 노드를 빠짐없이 채우되 반드시 끝까지 채울 필요는 없다.
이진검색트리(Binary Search Tree)란?
아래 조건을 만족하는 이진트리이다.
1. 어떤 노드 n을 기준으로 왼쪽 서브트리 노드의 모든 키값은 노드 n의 키값보다 작다.
2. 오른쪽 서브트리 노드의 키값은 노드 n의 키값보다 크다.
이진검색트리의 특징
- 구조가 단순하다.
- 중위 순회를 하면 키값의 오름차순으로 노드를 얻을 수 있다.
- 이진 검색과 비슷한 방식으로 아주 빠르게 검색할 수 있다.
- 노드를 삽입하는 것이 쉽다.
이진 검색트리의 단점
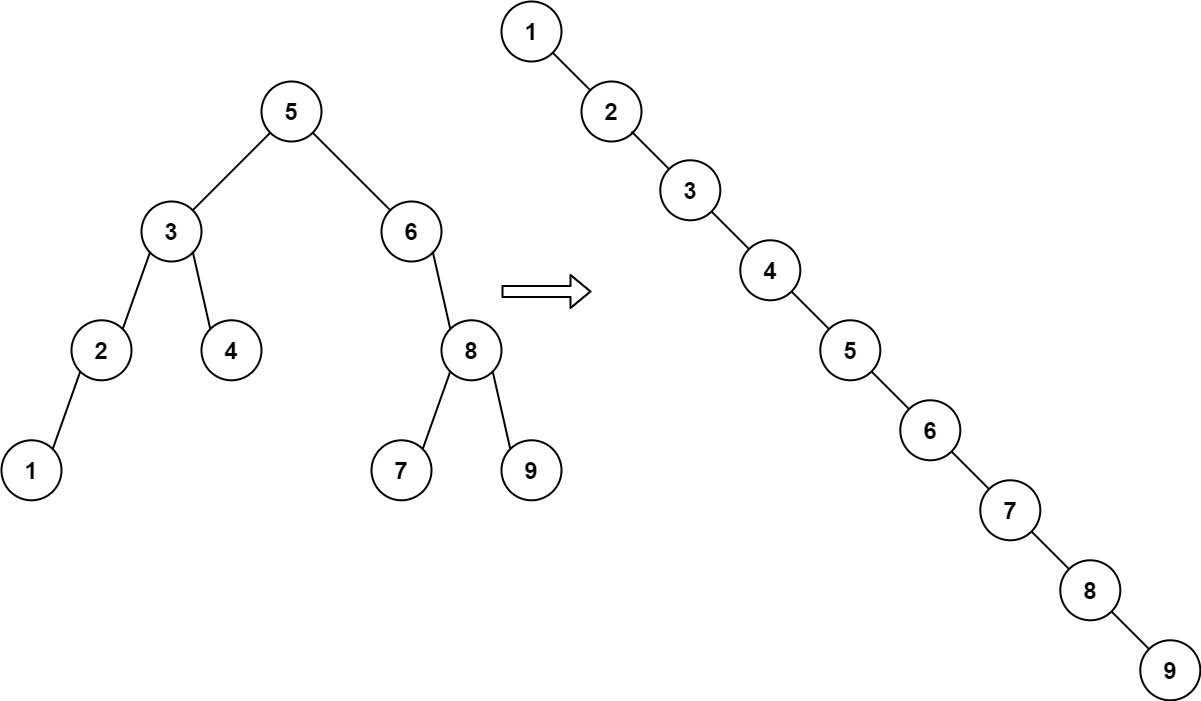
이진 검색트리는 검색, 삽입, 삭제하는 과정을 효율적으로 실행하지만, 키값의 오름차순으로 노드를 삽입하는 상황에서는 트리의 높이가 지나치게 커진다는 단점이 있다. 따라서 선형리스트와 같아지므로 빠른 속도로 검색할 수 없다.
균형검색트리(Self-blancing Search Tree)란?
균형검색트리는 높이를 O(log n)으로 억제하도록 고안된 구조로, 위에서 말한 이진 검색트리의 단점을 보완할 수 있다.
이진인 균형검색트리의 종류
- AVL 트리(ABL Tree)
- 레드-블랙 트리(Red-Black Tree)
이진이 아닌 균형검색트리의 종류
- B트리(B Tree)
- 2-3트리(2-3 Tree)
'프로그래밍👩🏻💻 > 자료구조' 카테고리의 다른 글
| [자료 구조] 그래프(Graph) (0) | 2022.07.28 |
|---|---|
| [자료 구조] 해시테이블(Hash Table) (0) | 2022.07.10 |
| [자료 구조] 연결 리스트(Linked list) (0) | 2022.07.09 |
| [자료 구조] Queue란? (0) | 2022.06.18 |
| [자료 구조] Stack이란? (0) | 2022.06.18 |




