suyeonme
[자료 구조] 그래프(Graph) 본문
그래프(Graph)란?
그래프는 정점(vertice)과 간선(edge)으로 이루어진 자료구조로, 트리(tree)도 그래프의 종류 중 하나이다. 하지만 그래프의 경우 정점마다 간선이 있거나 없을 수 있으며 루트 노드, 부모-자식이라는 개념이 존재하지 않는다.

그래프 사용 예시
포털 사이트의 검색 엔진, facebook의 네트워킹, 지하철 노선도등
그래프 관련 용어
| 용어 | 설명 |
| 정점(vertice) | 노드(node)라고도 하며 데이터가 저장된다. |
| 간선(edge) | 링크(arcs)라고도 하며 노드간의 관계를 나타낸다. |
| 인접 정점(adjacent vertex) | 간선에 의해 연결된 정점이다. |
| 단순 경로(simple-path) | 경로 중 반복되는 정점이 없는것, 즉 동일한 간선을 자나가지 않는 경로이다. |
| 차수(degree) | 무방향 그래프에서 하나의 정점에 인접한 정점의 수 이다. |
| 진출 차수(out-degree) | 방향그래프에서 사용되는 용어로 한 노드에서 외부로 향하는 간선의 수를 뜻한다. |
| 진입차수(in-degree) | 방향그래프에서 사용되는 용어로 외부 노드에서 들어오는 간선의 수를 뜻한다. |
| 사이클(cycle) | 한 정점에서 시작해서 해당 정점으로 끝나는 경로를 말한다. (A-B-C-D-A) |
| DAG(Directed Acyclic Graph) | 방향그래프이며 동시에 사이클이 존재하지않는 그래프를 말한다. 어떤 정점에서 출발해도 자기 자신으로 돌아오는 경로가 존재하지 않는다. |
그래프의 종류
방향그래프(Directed Graph) vs 무방향 그래프(Undirected Graph)
- 방향 그래프(Directed Graph): 간선에 방향이 있는 그래프이다.
- 무방향 그래프(Undirected Graph): 간선에 방향이 없는 그래프이다.

완전 그래프(Complete Graph)
각 정점에서 다른 모든 정점이 연결된 최대한 많은 간선수를 가진 그래프이다.
- 정점이 n개인 무방향 그래프에서 최대 간선 수 : n(n-1)/2 개, 5(5-1)/2 = 10개
- 정점이 n개인 방향 그래프에서 최대 간선 수 : n(n-1)개, 5(5-1) = 20개

부분 그래프(Sub Graph)
원래 그래프에서 일부 정점, 간선을 제외하고 만든 그래프이다.

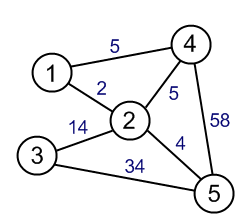
가중 그래프(Weight Graph)
정점을 연결하는 간선에 가중치를 부여한 그래프이다. 가중치 그래프는 네트워크(Network)라고도 불리운다.
예를 들어, 1지점에서 2지점까지 2km, 3지점에서 5지점까지34km의 거리를 나타내려면 간선에 가중치를 부여한다.
연결 그래프(Connected Graph) vs 비연결 그래프(Disconnected Graph)
- 연결 그래프: 서로 다른 두 꼭짓점이 연결되어 경로가 있는 그래프이다.
- 비연결 그래프: 서로 다른 꼭짓점중 연결되지 않은 정점이 있는그래프이다.

그래프 구현하기
인접 행렬(Adjacent Matric) 또는 인접 리스트(Adjacent List)를 이용하여 그래프를 구현할 수 있다.
인접 행렬(Adjacent Matric)
방향 그래프
- 그래프의 정점은 배열의 인덱스로 표현한다.
- 해당 정점에서 다른 정점으로 가는 간선(방향)이 존재하면 1, 그렇지 않으면 0으로 표현한다.
- 자기 자신으로 연결되는 경우는 존재하지않으므로 배열의 대각선은 모두 0이다.

무방향 그래프
- 그래프의 정점은 배열의 인덱스로 표현한다.
- 두 정점이 연결되어있다면 1, 그렇지 않으면 0으로 표현한다.
- 자기 자신으로 연결되는 경우는 존재하지않으므로 배열의 대각선은 모두 0이다.

인접 행렬 구현
public class Graph {
public static void print(int[][] graph) {
// 그래프 출력
for (int i = 1; i < graph.length; i++) {
for (int j = 1; j < graph.length; j++)
System.out.print(graph[i][j]+ " ");
System.out.println();
}
}
public static void putEdge(int[][] graph, int x, int y) {
// 정점 1과 3 사이의 간선이 존재하는 경우 : graph[1][3] = 1, graph[3][1] = 1
graph[x][y] = 1;
graph[y][x] = 1;
}
public static void main(String[] args) {
int n = 5; //그래프 정점의 개수
int[][] graph = new int[n+1][n+1];
putEdge(graph, 1, 2);
putEdge(graph, 1, 3);
putEdge(graph, 1, 4);
putEdge(graph, 2, 3);
putEdge(graph, 2, 5);
putEdge(graph, 3, 4);
putEdge(graph, 4, 5);
print(graph);
}
}인접 리스트(Adjacent List)
각 정점을 head로 시작해서 인접한 노드들을 전부 연결 리스트(Linked List)로 연결한다.

인접 리스트 구현
public class Graph {
public static void print(ArrayList<ArrayList<Integer>> graph) {
// 그래프 출력
for (int i = 1; i < graph.size(); i++) {
ArrayList<Integer> node = graph.get(i);
System.out.print("node"+"["+i+"] : ");
for (int j = 0; j < node.size(); j++)
System.out.print(node.get(j)+ "->");
System.out.println();
}
}
public static void putEdge(ArrayList<ArrayList<Integer>> graph, int x, int y) {
// 정점 1과 3 사이의 간선이 존재하는 경우 : graph.get(3).add(1), graph.get(3).add(1)
graph.get(x).add(y);
graph.get(y).add(x);
}
public static void main(String[] args) {
int n = 5; //그래프 정점의 개수
ArrayList<ArrayList<Integer>> graph = new ArrayList<>();
for (int i = 0; i <= n; i++) {
graph.add(new ArrayList<>());
}
putEdge(graph, 1, 2);
putEdge(graph, 1, 3);
putEdge(graph, 1, 4);
putEdge(graph, 2, 3);
putEdge(graph, 2, 5);
putEdge(graph, 3, 4);
putEdge(graph, 4, 5);
print(graph);
}
}인접 행렬 vs 인접 리스트
인접 행렬은 밀집 그래프(Dense Graph)를 표현하는데 효과적이다. 밀집 그래프란, 간선의 수가 정점보다 많은 그래프를 말한다.(e.g. 정점은 100개, 간선은 200개) 인접 행렬은 행렬을 사용하므로, 다른 정점과 연결되었는지의 여부를 판단할 때 인덱스를 사용한다. 따라서 복잡도는 O(1)이다. (인접 리스트는, head부터 타겟 노드를 찾을 때까지 탐색을 해야하므로 복잡도가 올라간다.)
인접 리스트는 희소 그래프(Sparse Graph)를 표현하는데 효과적이다. 희소 그래프란, 정점에 비해 간선이 적은 그래프를 말한다. (e.g. 정점은 100개, 간선은 5개) 연결 리스트를 사용하여 구현하면, 총 105개의 노드가 필요하다. (인접 행렬을 사용할 경우, 100x100 행렬이 필요)
그래프의 탐색

깊이 우선 탐색(Depth-first-search, DFS)
- 시작 정점으로부터 연결되어있는 다른 정점으로 계속 나아가고, 더 이상 나아갈 정점이 없다면 이전 정점으로 돌아가는 방식으로 그래프를 순회한다.
- 재귀 호출이나 스택을 사용하여 구현한다.
너비 우선 탐색(Breath-first-search, BFS)
- 시작 정점을 방문하고 시작 정점에 연결되어있는 모든 정점을 방문한 후 시작 정점에 인접한 모든 정점을 우선적으로 방문하여 그래프를 순회한다.
- 큐를 사용하여 구현한다. (지금 단계에서 방문할 수 있는 노드를 큐에 넣음)
'프로그래밍👩🏻💻 > 자료구조' 카테고리의 다른 글
| [자료구조/균형트리] B-트리, B+트리란? (0) | 2023.05.06 |
|---|---|
| [자료구조] 우선순위 큐(Priority Queue) (0) | 2022.11.06 |
| [자료 구조] 해시테이블(Hash Table) (0) | 2022.07.10 |
| [자료 구조] 트리(Tree) (0) | 2022.07.10 |
| [자료 구조] 연결 리스트(Linked list) (0) | 2022.07.09 |




