Notice
suyeonme
[알고리즘/그래프] 위상 정렬(Topology Sort) 본문
위상 정렬(Topology Sort)이란?
순서가 존재하는 작업을 수행할 때, 순서를 결정하기 위해 사용하는 알고리즘이다. 위상 정렬은 DAG(Directed Acyclic Graph, 방향성이 있으며 사이클이 없는 그래프)에만 적용할 수 있으며 여러개의 결과가 존재할 수 있다.
- 방향성이 있지만 사이클이 없어야 진입차수가 존재할 수 있다.
진입차수(in-degree), 진출 차수(out-degree)란?
- 진입차수(in-degree): A노드를 향하는(A노드로 들어오는) 간선의 개수
- 진출 차수(out-degree): A노드에서 외부로 향하는(나가는) 간선의 개수
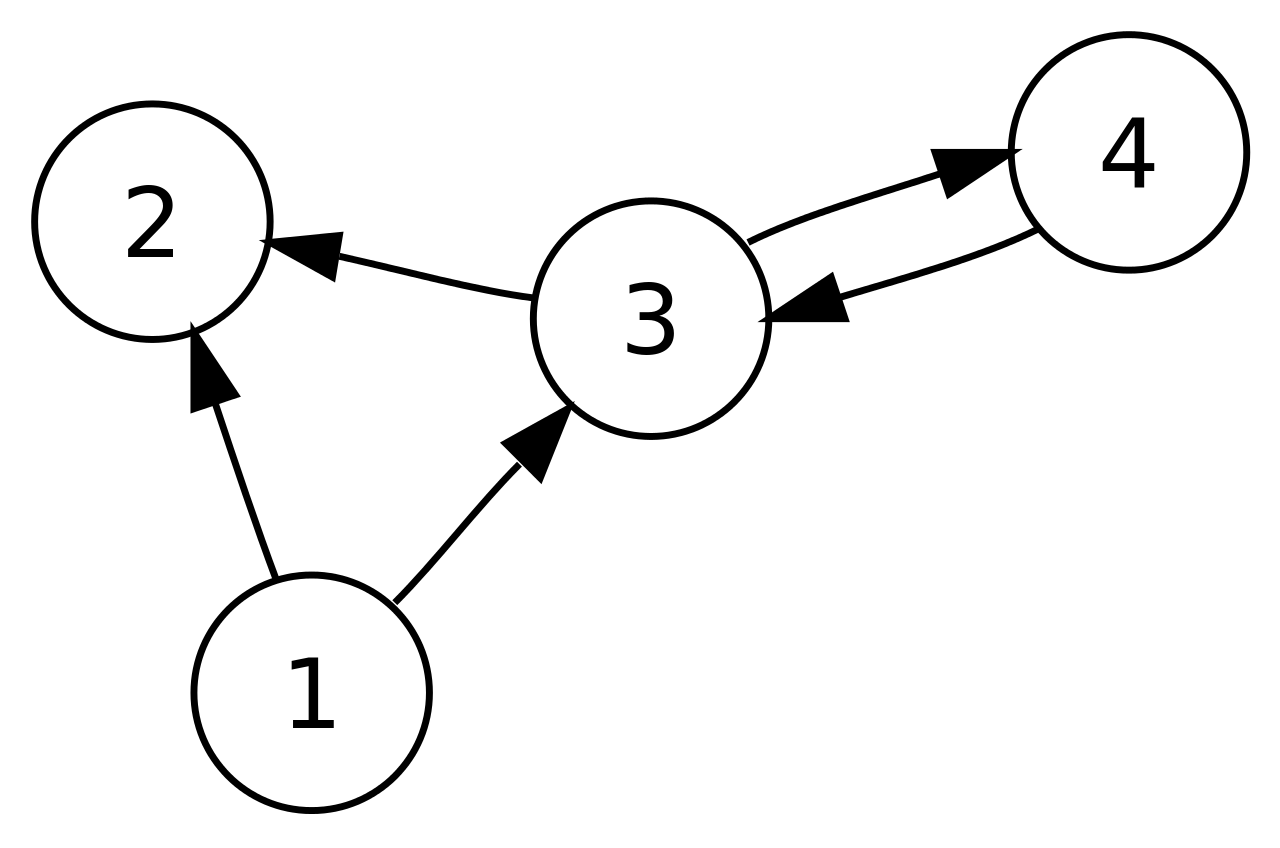
노드 2의 경우, 진입차수는 2, 진출차수는 0이다.
구현 방법
- Stack
- Queue
구현 순서
- 진입차수가 0인 정점을 큐에 삽입한다.
- 큐에서 노드를 꺼내서 연결된 모든 간선을 제거한다.
- 간선을 제거한 뒤, 진입 차수가 0이된 정점을 큐에 삽입한다.
- 큐가 빌 때까지 2~3번을 반복적으로 수행한다. 모든 노드를 방문하기 전에 큐가 빈다면 사이클이 존재하는 것이고 모든 노드를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과이다.
구현 코드
public class TopologySort {
public static int v; // 노드의 개수
public static int e; // 간선의 개수
public static int[] indegree = new int[100001]; // 진입차수
public static ArrayList<ArrayList<Integer>> graph = new ArrayList<ArrayList<Integer>>(); // 노드에 연결된 간선 정보
public static void topologySort() {
ArrayList<Integer> result = new ArrayList<>(); // 결과
Queue<Integer> q = new LinkedList<>();
// 진입차수가 0인 노드를 큐에 삽입
for (int i = 1; i <= v; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
// 큐가 빌 때까지 반복
while (!q.isEmpty()) {
int current = q.poll(); // 큐에서 원소를 꺼냄
result.add(current);
// 해당 원소와 연결된 노드들의 간선 제거(진입차수 -1)
for (int i = 0; i < graph.get(current).size(); i++) { // 연결된 노드만큼 반복
indegree[graph.get(current).get(i)] -= 1;
// 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if (indegree[graph.get(current).get(i)] == 0) {
q.offer(graph.get(current).get(i));
}
}
}
// 결과 출력
result.stream()
.map(integer -> integer + " ")
.forEach(System.out::print);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.println("v");
v = sc.nextInt();
System.out.println("e");
e = sc.nextInt();
// 그래프 초기화
for (int i = 0; i <= v; i++) {
graph.add(new ArrayList<Integer>());
}
// 방향 그래프의 모든 간선 정보를 입력 받기
for (int i = 0; i < e; i++) {
System.out.println("a");
int a = sc.nextInt();
System.out.println("b");
int b = sc.nextInt();
graph.get(a).add(b); // 정점 A에서 B로 이동 가능
// 진입 차수를 1 증가
indegree[b] += 1;
}
topologySort();
}
}'프로그래밍👩🏻💻 > 알고리즘' 카테고리의 다른 글
| [알고리즘/그래프] 에드몬드 카프(Edmonds-Karp) 알고리즘 (0) | 2022.12.04 |
|---|---|
| [알고리즘/그래프] 강한 연결 요소(Strongly Connected Component, SCC) (0) | 2022.11.20 |
| [알고리즘/그래프] 플로이드 와샬 알고리즘(Floyd Warshall Algorithm) (0) | 2022.11.06 |
| [알고리즘/그래프] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2022.11.05 |
| [알고리즘/그래프] 크루스칼 알고리즘(Kruskal Algorithm) (0) | 2022.10.31 |
Comments