Notice
suyeonme
[알고리즘/그래프] 에드몬드 카프(Edmonds-Karp) 알고리즘 본문
네트워크 플로우(Network-Flow) 알고리즘이란?
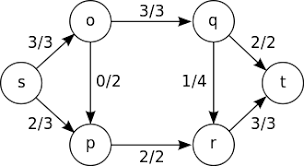
A지점에서 B지점으로 데이터가 얼만큼 많이 흐르고 있는지를 측정하는 알고리즘으로 , 최대 유량 문제(Maximum flow problem)를 해결하는데 사용된다. 최대 유량 문제란, 네트워크상에서 얼마나 많은 양의 데이터를 보낼 수 있는지,즉 최대 유량(Max Flow)을 찾는 문제이다. 최대 유량 알고리즘은 유량을 보내는 순서가 상관이 없다.
용어
- 유량(flow): 현재 흐르는 데이터의 양
- 용량(capacity): 간선에 흐를 수 있는 최대 데이터의 양
일반적으로 BFS(Breadth-first search)를 이용하며, 에드몬드 카프(Edmonds-Karp) 알고리즘이라고도 한다.
- 시간복잡도는 O(VE^2)이다.
- 도로의 교통 흐름, 전자 회로의 전류, 배수관을 흐르는 유량등을 분석하는데 사용된다.
에드몬드 카프(Edmonds-Karp) 알고리즘
- BFS를 이용하여 가능한 모든 경우의 수를 탐색한다.
- 현재 흐르고 있는 유량을 모두 0으로 설정한다.
- 가능한 용량(capacity)를 반복적으로 더한다. 이 때 가능한 capacity는 흘려보내는 경로의 유량중 가장 작은 유량이다.
- 남아있는 모든 경로를 계산하기 위하여 음의 유량을 계산한다. 즉 5만큼의 유량을 A에서 B로 보낸다면, B에서 A로 -5만큼의 유량을 보낸다고 할 수 있다.
구현 코드
package algorithm;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class NetworkFlow {
static int V = 7;
public static int[][] capacity = new int[V][V]; // 용량
public static int[][] flow = new int[V][V]; // 흐르는 유량
public static int[] visited = new int[V]; // 노드 방문 여부
public static int[][] graph = new int[V][V];
public static boolean bfs(int start, int end) {
Arrays.fill(visited, -1); // 모든 정점을 방문하지 않은 상태로 초기화
Queue<Integer> q = new LinkedList<Integer>();
q.add(start);
while (!q.isEmpty()) {
int x = q.poll();
System.out.println(x);
int[] target = graph[x];
for (int y : target) {
// 방문하지 않은 노드중 용량이 흐를 수 있는(남은) 경우
if (visited[y] == -1 && (capacity[x][y] - flow[x][y]) > 0) {
visited[y] = x; // 방문 처리, 경로 기억
q.add(y);
if (y == end) break; // 도착지에 도달
}
}
}
return visited[end] != -1;
}
public static int EdmondsKarp(int start, int end) {
int total = 0;
while (bfs(start, end)) {
int INF = Integer.MAX_VALUE;
// 거꾸로 최소 유량 탐색
for (int i = end; i != start; i = visited[i]) {
int x = visited[i];
INF = Math.min(INF, (capacity[x][i]) - flow[x][i]);
}
// 최소 유량 추가
for (int i = end; i != start; i = visited[i]) {
int x = visited[i];
flow[x][i] += INF;
flow[i][x] -= INF; // 음의 유량 탐색
}
total += INF;
}
return total;
}
public static void main(String[] args) {
graph[1][2] = 2;
graph[2][1] = 2;
capacity[1][2] = 14;
graph[1][4] = 4;
graph[4][1] = 4;
capacity[1][4] = 12;
graph[2][3] = 3;
graph[3][2] = 3;
capacity[2][3] = 5;
graph[2][4] = 4;
graph[4][2] = 4;
capacity[2][4] = 4;
graph[2][5] = 5;
graph[5][2] = 5;
capacity[2][5] = 6;
graph[2][6] = 6;
graph[6][2] = 6;
capacity[2][6] = 10;
graph[3][6] = 6;
graph[6][3] = 6;
capacity[3][6] = 8;
graph[4][5] = 5;
graph[5][4] = 5;
capacity[4][5] = 11;
graph[5][3] = 3;
graph[3][5] = 5;
capacity[5][3] = 4;
graph[5][6] = 6;
graph[6][5] = 6;
capacity[5][6] = 7;
int result = EdmondsKarp(1, 6);
System.out.println("최대 유량: " + result); // 최대 유량: 25
}
}'프로그래밍👩🏻💻 > 알고리즘' 카테고리의 다른 글
| [알고리즘/그래프] 이분매칭(Bipartite Matching) (0) | 2022.12.04 |
|---|---|
| [알고리즘/그래프] 강한 연결 요소(Strongly Connected Component, SCC) (0) | 2022.11.20 |
| [알고리즘/그래프] 위상 정렬(Topology Sort) (0) | 2022.11.07 |
| [알고리즘/그래프] 플로이드 와샬 알고리즘(Floyd Warshall Algorithm) (0) | 2022.11.06 |
| [알고리즘/그래프] 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2022.11.05 |
Comments